The Relation Between Story Points and Human Perception
Share
The relationship between story points and human perception is a really interesting topic. In the strict sense, the question at hand is why we use a representation of Fibonacci’s sequence when we are estimating the complexity of tasks in agile teams. Why do we use story points, and what makes story points a better tool than other estimation techniques? Those are questions answered in this article. The answers to those questions will give insight into the relation between human perception of the real world and the mathematical construct of Fibonacci’s sequence.
Effort Estimations Don't Work
One of the main reasons why effort estimations are not working is the way they are perceived by traditional managers. These managers do not consider classic effort estimates as estimates, they view them as a promise to complete the task in question within the estimated time. This leads to fear among developers that the estimates may be too optimistic. As a result, they integrate buffers in their estimates. This in turn means that the processing time actually increases. Experience shows that if a developer has six hours for a task, he will also use it up. Regardless of whether his original estimate was four hours or not. This “buffer creep” distorts the estimations, inflates and in the worst case, becomes uneconomical.
Secondly, cost estimates are never correct, because nobody can estimate the duration of a task exactly. As a result, developers experience a negative sense of achievement with every estimate. Furthermore, classic estimation methods leave no scope for risk assessment and the inclusion of uncertainties, ambiguities or potential stumbling blocks. Accordingly, they deviate massively from the later, actual processing time, especially for large problems.
The Cone of Uncertainty
A simple fact is expressed by the cone of uncertainty. The farther an event lies in the future, the less we know about it. As a result, our estimates of this event are inaccurate, blurry, or even incorrect. The closer we get to an event, the more we learn about it. This enables us to make better predictions and assumptions about this event. If we are very close to an event, there is almost no doubt about what will happen. For example, in an hour, in a minute or in the next second. Ultimately, any uncertainty has disappeared after an event has occurred. The event is history and cannot be changed.
This approach is also used to describe the possible effects of hurricanes. The picture shows the cone of uncertainty for hurricane Dorian from the Atlantic hurricane season 2019. As it can be seen, the possible corridor of the hurricane widens the further it is from the current location of the hurricane. This is due to the uncertainty regarding the weather influences on the future path of the hurricane.

This uncertainty can also be observed in software engineering. When developers are asked to estimate the delivery costs for certain requirements, this often works only to a limited extent. Because, the further the engineers are away from actually implementing these requirements, the more uncertain and inaccurate their estimates will be. They just don’t know the details and issues related to the specific implementation yet.

The greater the time lag between a developers estimation and the actual time of implementation, the greater the uncertainty and the risks. This requires finding an estimation model that takes this into account accordingly. Therefore, an approach that maps the cone of uncertainty is highly desirable.
Requirements for an Agile Estimation Technique
The above mentioned characteristics of classic effort estimations, and the knowledge about the Cone of Uncertainty, leave us looking for an estimation technique with the following features. The technique must not promote fear within the team. Furthermore, it must not allow the effect of “buffer creep”. Thirdly, it should take our knowledge about the Cone of Uncertainty into account. Finally, to incorporate those three requirements, it should allow the estimation of complexity instead of efforts.
The Golden Ratio
In order to get a grip on human perception of the real world we need to take a look at a very wide spread mathematical artifact. This artifact is called the Golden Ratio. In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Generally, this is the case when two quantities have a ratio of (1 + sqr(5)) / 2 = 1.618….
Interestingly, the Golden Ratio can be found almost anywhere in nature. It somehow resembles the key value of natural growth functions. Hence, humans have unconscious knowledge of the Golden Ratio. That’s why we perceive things that are in the Golden Ratio as natural and being in harmony. An example for this is the ratio of modern monitors and television sets. Due to technical limitations, the ratio of monitors has been 4:3 over several decades. The technology switch to LCD, TFT and LED panels has allowed to change the ratio to 16:9 or 16:10, which we perceive as much more comforting and natural.
Human Perception of the Real World
Another interesting concept is Fibonacci’s sequence. The sequence was named after Leonardo da Pisa, called Fibonacci. However, the sequence has already been known to mathematicians and philosophers in the ancient world. Fibonacci described this sequence of numbers using the example of a rabbit breeder who wants to find out how many pairs of rabbits arise from a single pair within a year if each pair gives birth to another pair per month from the age of two months. It turns out, that the number of bunny pairs in each generation is the sum of the previous two generations sizes.

Let’s have a look at the relationship between Fibonacci’s sequence and the Golden Ratio. The diagram shows the ratio of two adjacent elements of Fibonacci’s sequence in comparison to the Golden Ratio. It can be seen, that the ratio of Fibonacci numbers very quickly approaches the Golden Ratio. Technically speaking, the ratio of two adjacent elements alternates around the Golden Ratio. This means, that the elements of Fibonacci’s sequence resemble a growth function that is very closely related to the Golden Ratio. Eventually, Fibonacci’s sequence is a mathematical representation of natural growth functions.

The observed relation between Fibonacci’s numbers and the Golden Ratio leads us to the assumption, that the human perception of the real world follows the rules of Fibonacci’s sequence. For our whole life, we experience growth of populations, trees, flowers, and everything else that is created by nature, as something that follows the Golden Ratio. As we have seen, Fibonacci’s sequence is a very good mathematical representation of these natural growth functions. In this case, the usage of Fibonacci’s sequence for complexity estimations would relate to our natural, human understanding of magnitudes.
Fibonaccis Sequence and the Cone of Uncertainty
Now let’s take a look at how the Fibonacci sequence can be plotted against the cone of uncertainty. Is it able to cover the risk and inaccurate assumptions for distant future events? Are our estimations of problem sizes really related to the natural, human understanding of growth functions? As it can be seen, the Fibonacci sequence actually covers the cone of uncertainty very well.
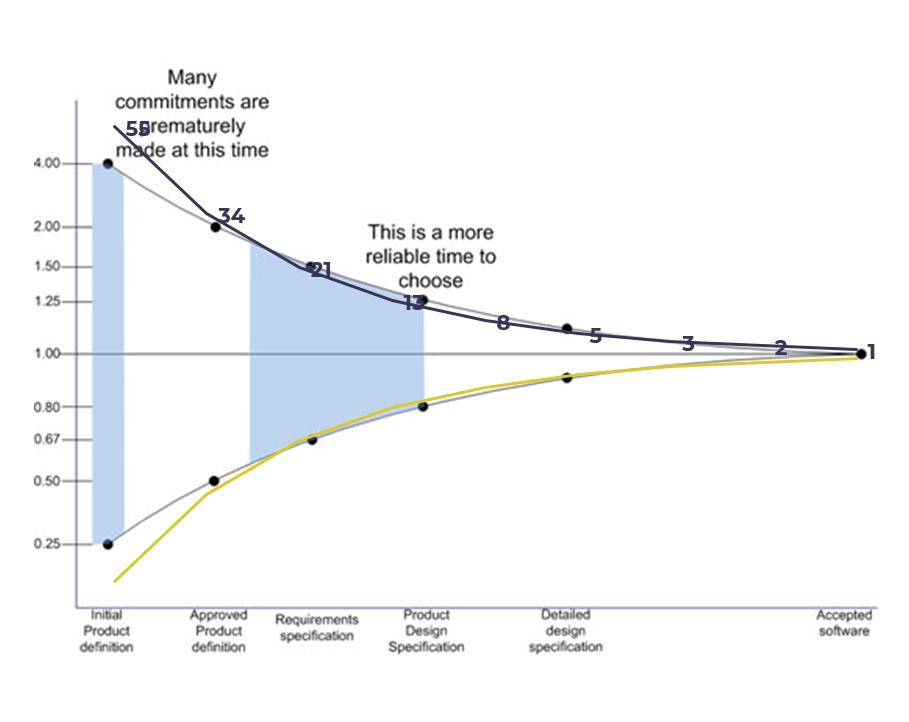
This diagram shows us a lot about the grade of maturity of requirements. A requirement, or user story which is estimated as one, two or three points is well refined and implementation can be started. Requirements with a complexity of five or eight story points are almost ready for implementation, but have to be split a little further. All tasks that are estimated with thirteen or more story points are still far from being implemented. The risk and uncertainty is still too big. Those requirements have to be discussed and refined much more. This is the point where decisions about system design and architecture are made.
Story Points Match Human Perception
Considering the above mentioned facts about human perception, natural growth and their relation to Fibonacci’s sequence, we can link all of those aspects together. We have seen, that Fibonacci’s sequence oscillates around the golden ratio. At the same time, Fibonacci’s sequence also maps almost perfectly to the Cone of Uncertainty.
On the other hand, humans are well used to natural growth functions from their every day life. Hence, their estimations of magnitudes follows the golden ratio. Thus, those estimations create the Cone of Uncertainty in a way that is related to natural growth functions, which are resembled by Fibonacci’s sequence.

This leads us to the final conclusion. Because we are humans, we are used to estimate magnitudes in a way that is related to natural growth functions. A mathematical representation of those growth functions is Fibonacci’s sequence. Hence, it is very beneficial to use the elements of Fibonacci’s sequence as representative values for complexity estimations. In practice, this leads us to the usage of Story Points for our estimations.
Final Thoughts
In this article, we have discussed how human perception of the real world and Story Points relate to each other. Fibonacci’s sequence is a mathematical representation of natural growth functions. Hence, we all have an intuitive understanding of the sequence. Using this sequence as values for Story Points makes it intuitive for developers to estimate the complexity of problems. Concluding, and in the style of famous statesman Winston Churchill, it can be said that: No one pretends that Story Points are perfect or all-wise. Indeed, it has been said that Story Points are the worst form of agile estimation except all those other estimation techniques that have been tried from time to time.